Equipotential Chess

After a few weeks' worth of playtesting (spanning several months of nonoverlapping schedules), I'm proud to release a new board game into the wild, based on some really nice physics.

For the uninitiated, equipotentials are surfaces of constant potential energy, and field lines (prominent examples of which have probably surfaced in your childhood education vis-a-vis magnets) show the direction of the net force from a particular field. Properly constructed, equipotentials and field lines should in principle be orthogonal everywhere they intersect — just like lines on a chessboard. In fact, exactly like lines on a chessboard…

A beginner's beginners' guide to 象棋

象棋, or Chinese chess, is a quasi-popular pastime among Singaporeans¹. The most obvious difference between it and international chess is that pieces are played on the intersections of grid lines, instead of inside cells defined by grid lines. For an ordinary square board, this difference is trivially superficial (just like the difference between contravariance and covariance is unimportant in Euclidean space). However, for alternative topologies, things like the two-colouring scheme imposed by a flat orthogonal grid cannot necessarily hold, and things might get interesting — that is to say, too interesting for things like Bishops to work properly. On the other hand, if we can guarantee orthogonality of grid lines at least locally, then we can still play a game with Chinese chess-like rules irrespective of the global topological structure.

Rather than insult the reader's ability to read Wikipedia, we shall merely summarise. In Chinese chess, all moves consist of a single uninterrupted line segment of arbitrary length along grid lines, which may or may not terminate with a capture, with some exceptions:

1. Pawns （兵/卒） may only take steps of unit length; moreover they cannot move backwards at any point, and may move sideways only after crossing the central river;
2. Horses （马） may only make a compound move consisting of first a unit step, and then movement across a diagonal such that the overall path bounds two cells (this is similar to the Knight movement mechanic in international chess); a piece blocking the first unit step precludes the second part of the move (顶马脚)
3. Elephants （相/象） may only make two successive diagonal movements in the same direction along the same diagonal; once again, an intervening piece renders a move invalid. Also they can't cross the river because your generals are not as batshit as Hannibal.
4. Palace Guards （士/仕） may only make unit steps along certain designated diagonals that are marked out on the board;
5. Cannons （炮/砲） may only capture a piece by jumping over exactly one intervening piece;
6. The General （将/帅） may only take unit steps inside of the Palace. Additionally, line-of-sight between Generals counts as check for endgame purposes (飞将).

In retrospect, that's a lot of exceptions.

Equipotentials

We generate our board by considering the net field and effective equipotentials produced by two co-orbiting bodies of equal mass $m$, resulting from both the gravitational force and centrifugal effects. In the rotating barycentric reference frame, the effective potential is given by

where $\hat{\mathbf{n}}$ is a unit vector denoting the axis of rotation, $a$ is proportional to the gravitational term $Gm$, and $b$ gives us the effective centrifugal potential $\frac{1}{2}\omega^2$. This gives us a playing field that is both rotationally symmetric around the axis connecting the two masses, and reflectively symmetric about the plane at the midpoint of the system bisecting this axis. Projecting onto two dimensions gives us something that looks like this:

This is actually half the board; the actual board possesses mirror symmetry around the central plane (represented by the line on the right). There are a few immediately interesting features:

1. All equipotentials (the circles and roundish curves) intersect the field lines (the radial curves) at right angles everywhere
2. There are vertices where field lines intersect; for gameplay purposes, we treat them as ordinary vertices, with straight line segments being interpreted geometrically. The most obvious one is where all the field lines come together in the middle. These are source/sink singularities, and they correspond to where the point masses (planets?) would be. As such, Generals start there.
3. We've marked out the first equipotential (corresponding to a LEO-like positioning) and the sixth with double lines. We'll get back to this later.
4. On the right side of the board, there is another vertex where field lines intersect. However, we see that the vertical field lines converge there, but the horizontal ones diverge! As it turns out, this is a (gravitational) saddle point, just like all the Lagrange points (except L4/5) are; in particular, this is the L1 Lagrange point for these two bodies. The equipotentials here represent Lissajous orbits that are stable around the axis, but unstable along the axis.
5. Finally, we see that there exist both cells with three sides (adjoining the point mass) as well as five (near the saddle point). This forces us to redefine “diagonal” for gameplay purposes.

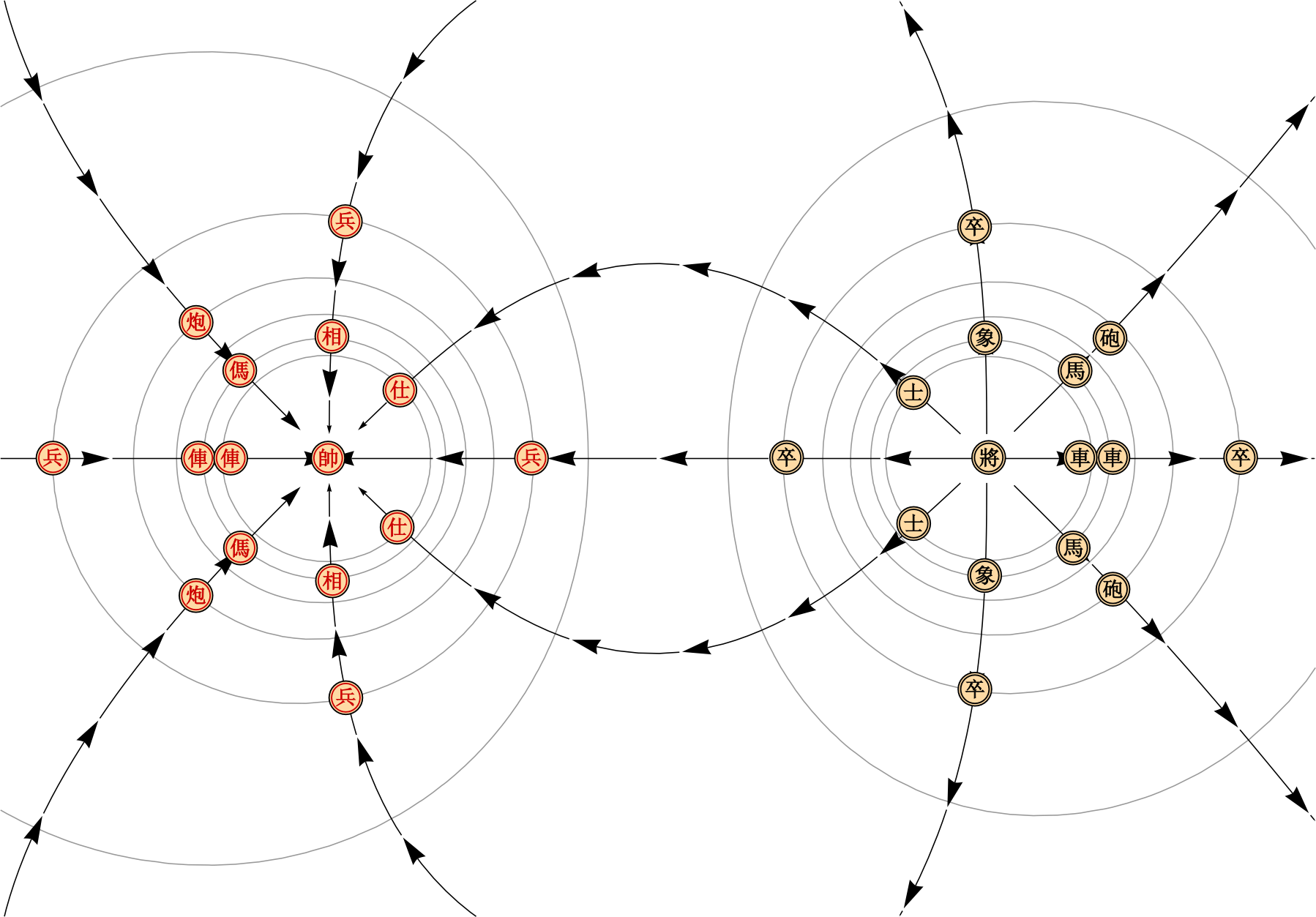
After quite a bit of playtesting and rebalancing, we settled on the following layout for pieces:

The topology of this setup differs pretty significantly from the flat board. Consequently, there must exist some deviations from standard gameplay rules:

1. Instead of advancing forward by unit steps, pawns advance along field lines either out of your own gravitational well, or into your opponent's gravitational well. Once in your opponent's gravitational well, a pawn can also take unit steps along equipotentials.
2. The sixth equipotential (marked with a double line) is special; pawns may move freely along it, as long as their path is not interrupted. However, they still may not capture nonadjacent pieces (except other pawns).
3. Pawns and Elephants may not advance past the sixth equipotential.
4. As there are no Palace diagonals to speak of, Palace Guards may move freely along the first equipotential (marked with a double line), so long as their path is not interrupted. They may also take a unit step down to the planet, or back up to low-earth orbit.
5. We define diagonal movement as movement along two consecutive edges, both bounding the same cell. Thus, if I were to begin on one vertex of a triangle, a diagonal movement entitles me to end up at either of the other two vertices; conversely, if I were to begin at one vertex of a pentagonal cell, the two vertices adjacent to me are inaccessible by diagonal movement. In particular, moves for Horses and Elephants will use this definition of diagonality.

Rules aside, the new topology leads to some pretty interesting situations. For example, a single Chariot can threaten an enemy piece on an otherwise empty equipotential from two different directions. We leave the discovery of more interesting tactical and strategic consequences as an exercise for the reader.

Generalisations

Obviously, this also means that we can turn arbitrary physical configurations into playable chessboards:

Antigravity

Space Yugoslavia

The possibilities are technically endless, right?

More stuff?

During playtesting, I received a lot of feedback that the game would have been easier to pick up had it been computerised. Prima facie, this seems like a pretty good idea; however, the presence of singularities where field lines intersect (i.e. the field sinks and saddle points) makes parameterisation difficult. If anyone has any ideas as to how to implement this properly (or really any feedback on the game in general), feel free to leave a comment.

Update 3rd August 2016: I've created a computerised version of this game! Right now it's a preliminary sketch that doesn't have support for some important features (game save/load, game reset, AI, network play… actually that's a lot of features). The computerised version can be found at its GitLab repo.

Resources²

These boards were generated in Mathematica with $a=1,b=0.125$, and are designed to be played with smallish pieces when printed at size A2.

• Half Board (useful for printing boards larger than your printer allows; just print two copies and join them together)
• Half Board Layout
• Full Board
• Full Board Layout

Acknowledgements

Many thanks are owed to Kho Zhe Wei, Ernest Tan, and everyone else who played this game and/or offered feedback on it of some sort. Thanks also to YCX and KLKM, who tested the computerised version.