Computer-Assisted Feng Shui

When I first arrived in Hawaiʻi, I had only two weeks within which to find a place to transfer all my belongings to before having to leave again for Maryland to attend the Hubble Symposium, so as not to pointlessly burden my gracious hosts. With such a short runway, I effectively picked the first apartment that I viewed that wasn't a mold-ridden insect-fest. While I'm not terribly unhappy with my current place, however, I might have made a mistake in the arrangement of my furniture. Having placed my desk against the Eastern wall of the apartment, I was for the first month or so plagued by monitor glare caused by reflected sunlight near sunset. Since my work desk is chiral, moving it to the Western wall would require me to completely disassemble it, and then put it back together in the opposite chirality. Fortunately, this glare has gone away as the Sun has set in a more and more southerly direction over the course of the past winter months. Nonetheless, I would like to assess how much of a problem this might be in the coming summer months, and whether I should “eat the frog”, such as it is, and rearrange all of my furniture to accommodate a West-facing desk.

To do this, I calculate the times of year in which the Sun lies in a problematic area of sky. We first begin by writing down the position of the Sun in terms of its current declination $\delta$ (depends on time of year), our current latitude $\lambda$, and the hour angle of the Sun $H$ (0 at zenith, defined positive towards sunset). From high school celestial mechanics, we eventually recall that

and

where $\alpha$ and $\phi$ are the altitude and azimuth.

import numpy as np
import matplotlib.pyplot as plt

def solar_azimuth(lat, decl, H):
    '''
    Given a latitude, solar declination, and hour angle,
    compute the solar azimuth.
    '''

    sin_α = np.sin(decl) * np.sin(lat) + np.cos(decl) * np.cos(lat) * np.cos(H)
    cos_α = np.cos(np.arcsin(sin_α))
    sin_φ = -np.cos(decl) * np.sin(H) / cos_α
    cos_φ = (np.sin(decl) - np.sin(lat) * sin_α) / (np.cos(lat) * cos_α)
    return np.arctan2(sin_φ, cos_φ)

def solar_altitude(lat, decl, H):
    '''
    Given a latitude, solar declination, and hour angle,
    compute the solar altitude.
    '''
    sin_α = np.sin(decl) * np.sin(lat) + np.cos(decl) * np.cos(lat) * np.cos(H)
    return np.arcsin(sin_α)

def sunset_hour_angle(lat, decl, α0=0):
    '''
    Hour angle of the Sun at sunset (defined to be at altitude α0,
    not necessarily 0)
    '''
    return np.arccos((np.sin(α0) - np.sin(decl) * np.sin(lat)) / (np.cos(decl) * np.cos(lat)))

DEGREES = 2 * np.pi / 360

Let us also save some important facts somewhere. We compute the declination as a function of time of year. We also describe the latter in terms of month number (1 = January, etc.) for easy interpretation of the subsequent figures. We consider only reasonable values of the hour angle (so that we don't waste time thinking about what happens at night, when solar glare is not a concern). We note that our latitude (Honolulu) is a constant of the problem. Finally: from Google Maps I measure the normal vector of my Northern wall to point at bearing 341 degrees.

θ_equinox = (31 + 28 + 20) / 365.25 * 2 * np.pi # date of vernal equinox in radians
θ = np.linspace(0, 2 * np.pi, 366)[:-1] - θ_equinox # θ = 0 is the vernal equinox
m = np.linspace(0, 12, 366)[:-1] + 1

ε = 23.4363 * DEGREES # Earth's obliquity
δδ = np.arcsin(np.sin(ε) * np.sin(θ))

hh = np.linspace(-2, 2)

λ = 21.315603 * DEGREES # Honolulu

φ0 = (341.84 - 360 - 90) * DEGREES # orientation of 1550 Wilder Ave

With all this infrastructure in hand, let's first examine how the solar azimuth varies over the course of the day and year. I show this angle with a cyclic colourmap, and over it I plot the hour angle at which the Sun rises and sets, as a function of the time of year.

φ = solar_azimuth(λ, δδ[None, :], hh[:, None])

plt.pcolormesh(m, hh, φ, cmap='twilight')
plt.plot(m, -sunset_hour_angle(λ, δδ), label='Sunrise')
plt.plot(m, sunset_hour_angle(λ, δδ), label='Sunset')
plt.xlabel('Month')
plt.ylabel('Hour Angle')
plt.colorbar(label=r"Azimuth/rad", pad=.01)
plt.show()

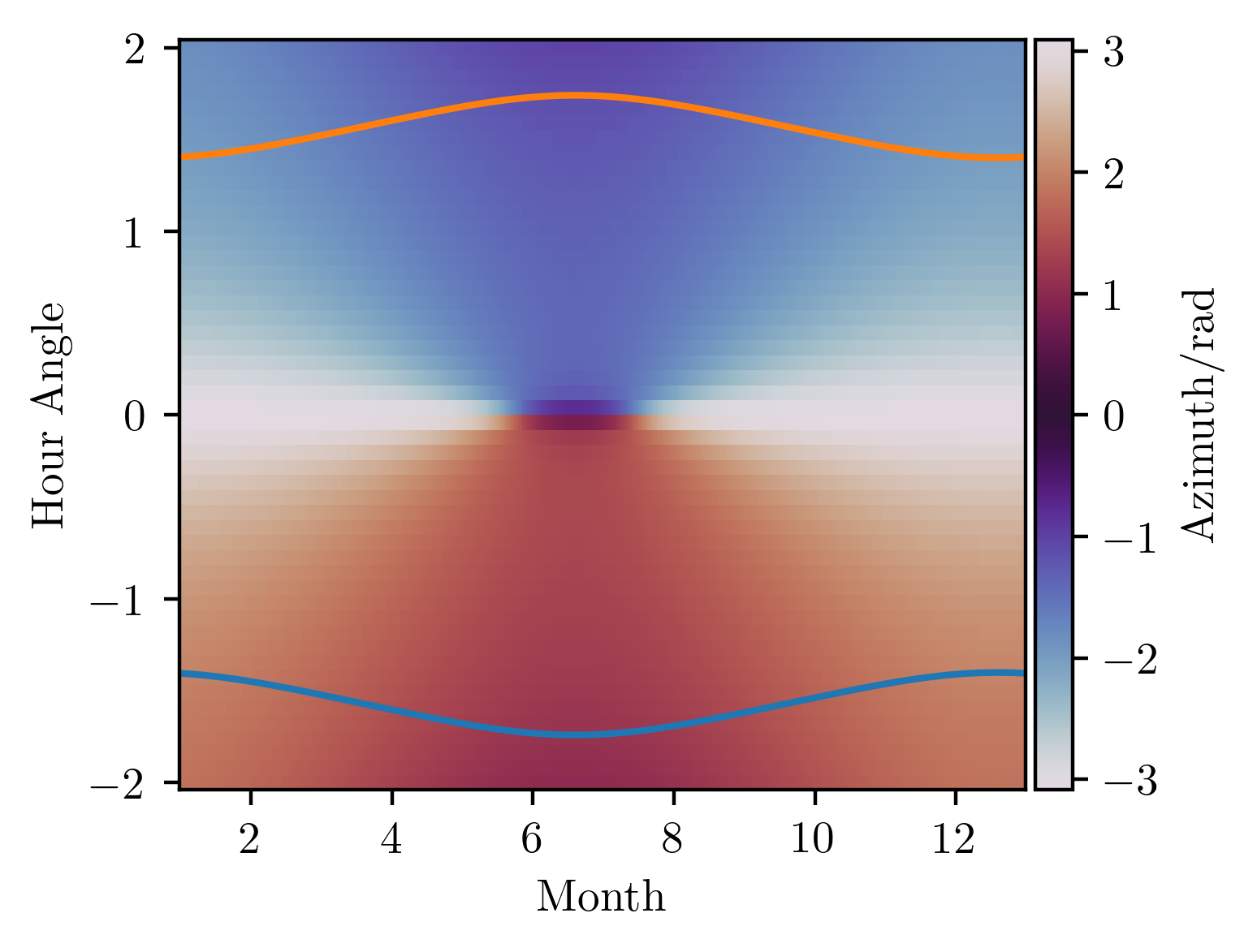
What we're actually interested in, however, is the azimuth of the Sun at sunset (i.e. the azimuth values evaluated along the "sunset" curve). I now also introduce some information about my workspace geometry into the problem, since, far enough into the summer, the Sun sets far enough North that it strikes my monitor at a glancing angle at sunset, so that I no longer am affected by glare.

plt.plot(m, solar_azimuth(λ, δδ, sunset_hour_angle(λ, δδ, α0=0 * DEGREES)))
plt.axhline(φ0, label='North Wall', ls='dashed', c='gray')

As measured from my eyes, to the centre of my monitor, to the edge of my monitor, and back my workspace configuration describes a right-angled triangle of 30 inches, 14 inches, and 33 inches (I don't own a cm tape rule).

θ_glare = np.arctan(14 / 30)
plt.axhspan(φ0, φ0 + θ_glare, alpha=.1)

My monitor is also 7.9 inches high, but I want to say that my centreline is already inclined 10 degrees down from the horizontal.

α_glare = np.arctan(7.9 / 30) + 10 * DEGREES

plt.legend()
plt.xlabel('Month')
plt.ylabel('Azimuth/rad')
plt.show()

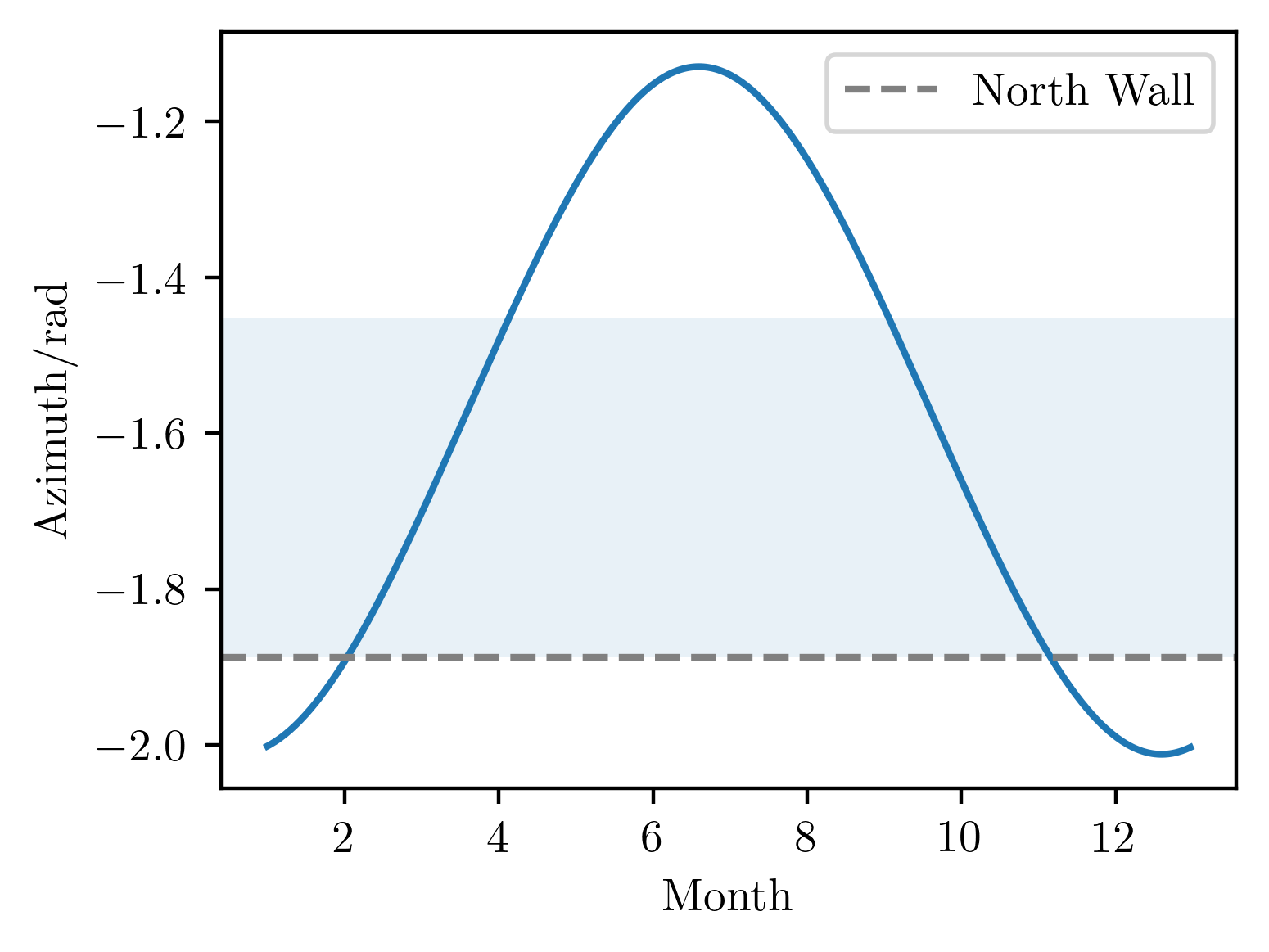
We see that glare will be a problem at sunset between February and April, and again between September and November. During the winter months, the Sun is further south than the line of the North Wall, and cannot be seen at sunset. During the summer months, the Sun sets far enough North that glare is not a problem at sunset.

However, even though the Sun sets too far North to cause glare at sunset for a while after April, it might cause glare shortly before sunset then (when it's higher up in the sky, while being further south). Thus, we also need to consider the altitude of the Sun over time as well. At this point, we further recall that

which we will use to solve numerically for $\alpha$ as a function of $\phi$ (i.e. without explicit dependence on the hour angle) by bisection. First, let us have a look at the discriminant function implied by this identity.

from scipy.optimize import bisect

def discr(decl, lat, φ, α):
    return np.sin(decl) - np.sin(lat) * np.sin(α) - np.cos(lat) * np.cos(α) * np.cos(φ)

def alt_at_azimuth_(decl, lat, φ):
    def d(α):
        return discr(decl, lat, φ, α)
    try:
        return bisect(d, 0, np.pi/2)
    except ValueError:
        return np.nan

alt_at_azimuth = np.vectorize(alt_at_azimuth_)
plt.pcolormesh(m, np.linspace(0, np.pi/2), discr(δδ[None, :], λ, φ0,
               np.linspace(0, np.pi/2)[:,None]), vmin=-1, vmax=1, cmap='RdBu')
plt.colorbar(label=r"Discriminant at $\phi_0$", pad=.01)
plt.ylabel(r"Altitude/rad")
plt.xlabel(r"Month")
plt.show()

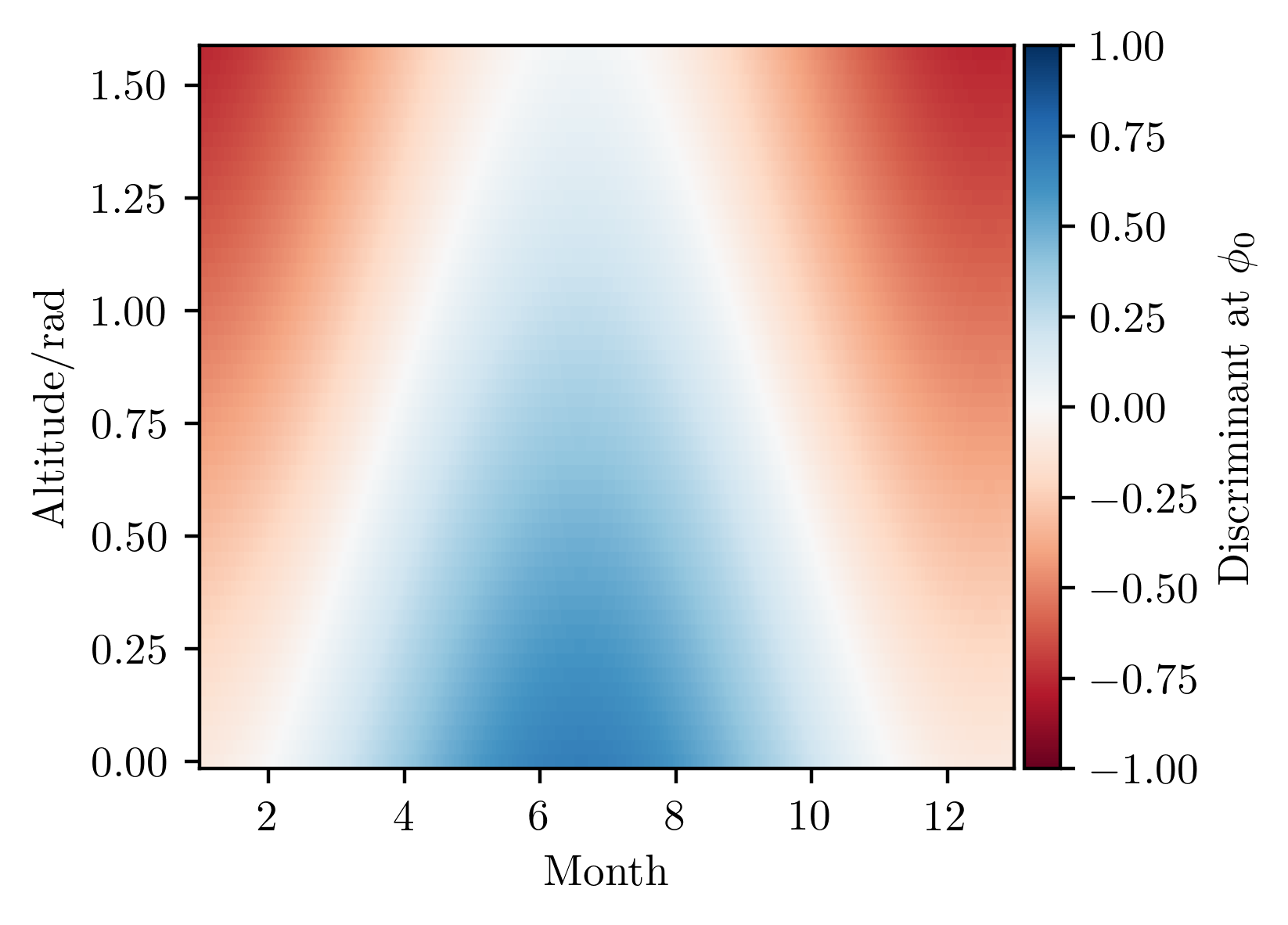
For any given declination, the corresponding altitude at the specified azimuth lies on the loci specified by where this discriminant function goes to 0 (the white area of the figure). However, we see that not all days of the year have a well-defined altitude: this means that on these days, the Sun never crosses the specified value of the azimuth during the daytime.

With this in hand, we are now better-equipped to consider the possibility of glare at times other than sunset.

plt.plot(m, alt_at_azimuth(δδ, λ, φ0), label='Shadow of window')
plt.plot(m, alt_at_azimuth(δδ, λ, φ0 + θ_glare), label='Left edge of monitor')

plt.axhline(α_glare, ls='dashed', label="Top edge of monitor")

plt.fill_between(
    m, np.minimum(α_glare, alt_at_azimuth(δδ, λ, φ0)),
    np.minimum(α_glare, np.nan_to_num(alt_at_azimuth(δδ, λ, φ0 + θ_glare))),
    alpha=.1, label='Glare'
)

plt.legend(ncol=2, loc='upper center', bbox_to_anchor=(.5,1.2))

plt.xlabel('Month')
plt.ylabel('Altitude/rad')
plt.show()

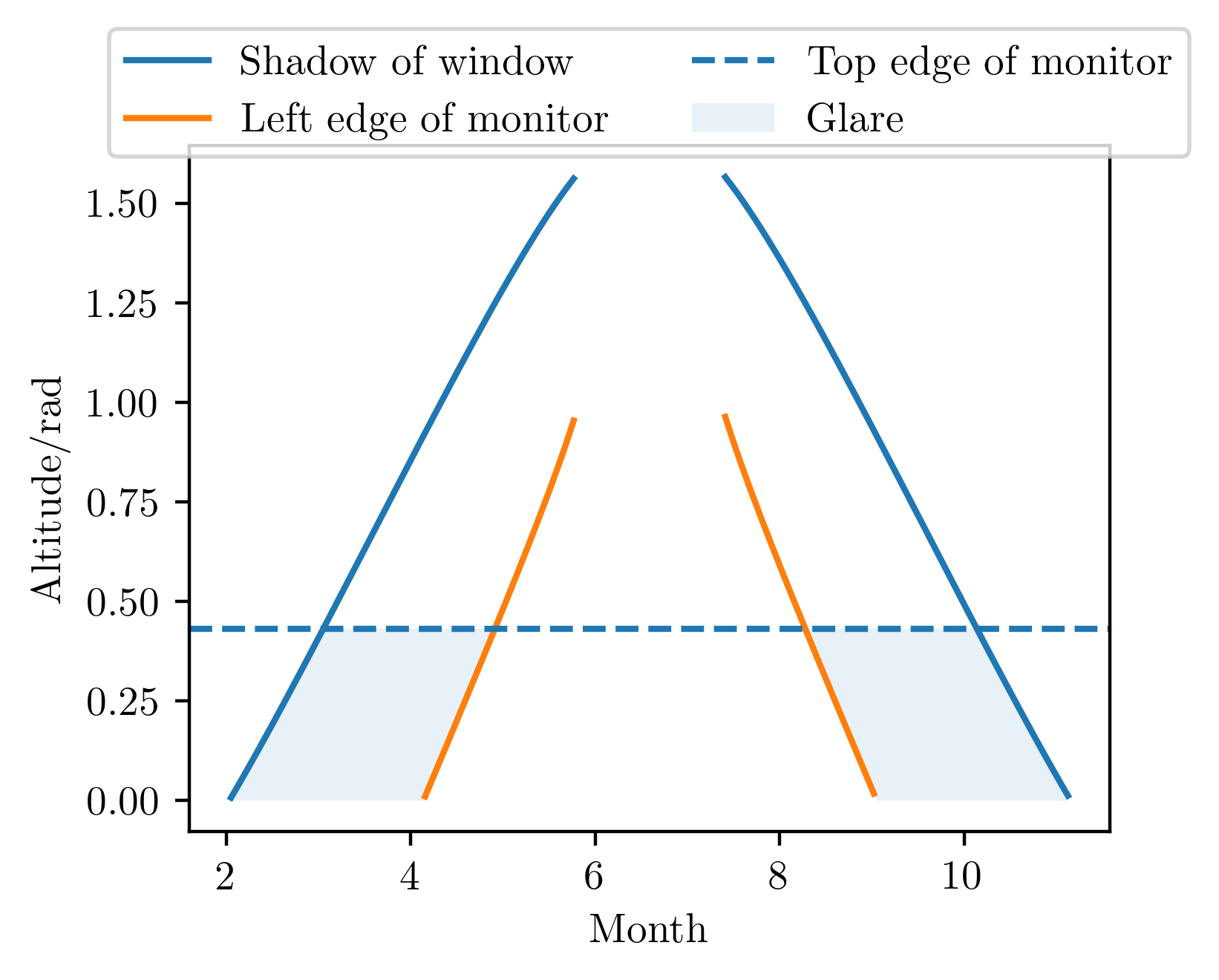
This figure takes a bit of work to unpack:

• The blue solid curve shows the altitude of the Sun when the line of sight is parallel to my Northern wall. When the Sun is further north than this, rays are cast on my monitor, and I might get glare. As such, only points below this curve are a cause for concern.
• The orange solid curve shows the altitude of the Sun when the line of sight is such that the reflection barely can be seen on the left edge of my computer monitor. When the Sun is further north than this, the reflected rays from my monitor all miss my eyes to the right, and I get no glare. As such, all points below this curve are safe, and yield no glare.
• The blue dashed line shows the altitude of the Sun when the line of sight is such that the reflection barely can be seen on the top edge of my monitor. When the Sun is higher than this, the reflected rays from my monitor all fall below my eyes, and I get no glare. As such, all points above this line also yield no glare.

Thus, I will only experience monitor glare when the Sun lies in the shaded region. Fortunately, this means that I will only meaningfully experience glare for a couple of months, twice a year: from around early Feburary to late April in the Spring, and the converse dates (flipped around Summer solstice) in the Fall. This is probably bearable, especially seeing as I will be in the office for most of the work day anyway.

What does the comparable situation look like if I had placed my desk up against the Western wall to begin with?

plt.plot(m, alt_at_azimuth(δδ, λ, φ0 + np.pi), label='Shadow of window')
plt.plot(m, alt_at_azimuth(δδ, λ, φ0 + np.pi - θ_glare), label='Right edge of monitor')

plt.axhline(α_glare, ls='dashed', label="Top edge of monitor")

x = alt_at_azimuth(δδ, λ, φ0 + np.pi)
x[np.isnan(x) & (m > 5.5) & (m < 7.5)] = np.pi/2

plt.fill_between(
    m, np.minimum(α_glare, x),
    0,
    alpha=.1, label='Glare'
)

plt.legend(ncol=2, loc='upper center', bbox_to_anchor=(.5,1.2))

plt.xlabel('Month')
plt.ylabel('Altitude/rad')
plt.show()

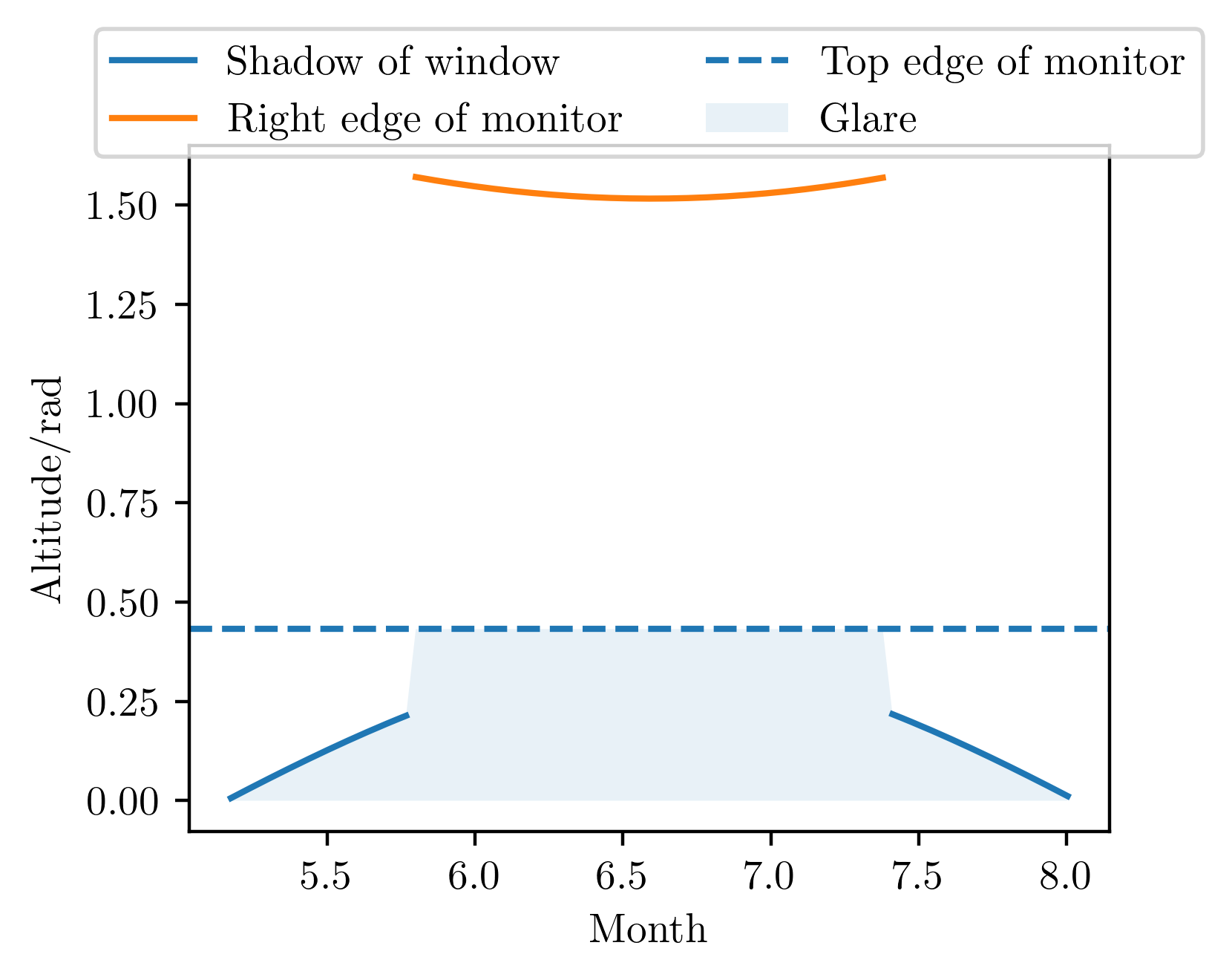
Rather than glare at sunset, I would encounter monitor glare at sunrise. During the winter, the Sun is too far south to illuminate the monitor during the morning. However, in the Spring, there will come a day where the Sun rises in line with the Eastern wall. As the Sun rises at an increasingly Northern point on subsequent days, more and more of the morning will be spent with monitor glare before the Eastern wall finally casts a shadow on the monitor. Far enough into Summer, the Sun spends the entire day far North enough that the shadow cast by the Eastern wall never falls on the monitor — that is, the Sun would actually lie in the problematic azimuthal range all morning! On such days, by the time the reflection of the Sun moves off the right edge of the monitor (if it does at all; orange curve), it will be late enough in the day that it won't matter. As such, I will spend about 2.5 months suffering from sunrise glare were my desk to face West, compared to the 4 that I currently would suffer from sunset glare with my desk facing East.

This is a tough choice! I think what I will do is tough out the coming Spring sunset glare, and then commit to inverting the chirality of my desk only after this August, once the sunrise glare abates.